How to Measure Angles in a Polygon? Expert Tips & Tricks

To measure angles in a polygon, you need to know a few basic rules. Each type of polygon has its own set of guidelines for angle calculation.

Understanding how to measure angles in a polygon is essential for many fields, including geometry, engineering, and architecture. Whether you are a student, a professional, or just curious, knowing how to measure these angles can be very useful. In this guide, we’ll break down the steps and rules for measuring angles in different types of polygons.

From triangles to hexagons, you’ll learn the simple methods to calculate each angle accurately. Get ready to improve your understanding of polygons and their angles!

Credit: study.com

Introduction To Polygon Angles

Hey friends, today we’re diving into the world of polygons. These shapes are everywhere, from your home walls to the design of your favorite video games. But how do we measure the angles in these shapes? It’s simpler than you think, and I’ll guide you through it step by step. First, let’s understand what polygons are and why knowing their angles is important.

Definition Of Polygons

So, what exactly is a polygon? A polygon is a flat shape with straight sides. Think of a triangle, a square, or even a pentagon. If it has straight sides and is closed (meaning all the sides connect), it’s a polygon. Here’s a quick list of common polygons:

• Triangle: 3 sides
• Square: 4 sides
• Pentagon: 5 sides

Easy, right? The sides of a polygon meet at points called vertices. And the angles we’re talking about are formed at these vertices.

Importance Of Measuring Angles

Now, why should we care about measuring these angles? Well, understanding angles helps in many ways:

• Building and Construction: Ensuring structures are safe and stable.
• Design: Creating patterns and designs that are visually pleasing.
• Navigation: Maps and GPS systems rely on accurate angle measurements.

Think about it. If you’re building a house, you need to know the angles to make sure the walls are straight and the roof fits perfectly. Or, if you’re designing a game, knowing angles helps to create realistic environments.

I remember when I was working on a school project, building a small model house. I didn’t measure the angles correctly, and the roof ended up looking lopsided. That was a hard lesson learned! But it showed me how crucial it is to get those angles right.

So, ready to learn how to measure these angles? Stick with me, and I’ll show you the ropes. It’s easier than you think and super useful in everyday life!

Types Of Polygons

Understanding the types of polygons is crucial. It helps in measuring angles accurately. Polygons come in various shapes and sizes. Each type has unique properties.

Regular Vs Irregular Polygons

Regular polygons have all sides and angles equal. Think of a square or an equilateral triangle. These shapes are symmetric. Measuring angles in regular polygons is straightforward.

Irregular polygons have sides and angles of different lengths and sizes. An example is a scalene triangle. These shapes lack symmetry. Measuring angles in irregular polygons needs more steps.

Convex Vs Concave Polygons

Convex polygons have all interior angles less than 180 degrees. A pentagon is a good example. These polygons bulge outward. Measuring angles is simpler in convex polygons.

Concave polygons have at least one interior angle greater than 180 degrees. Think of a star-shaped polygon. These polygons have an inward dent. Angle measurement in concave polygons can be tricky.

Basic Angle Measurement Tools

Hey friends, today we’re diving into the basics of measuring angles in a polygon. Understanding the right tools to use can make this task much easier. Whether you’re a student, teacher, or just curious about geometry, knowing how to measure angles accurately is important. Let’s talk about two basic tools: the protractor, and the ruler and compass.

Protractor Usage

The protractor is a classic tool for measuring angles. It’s simple to use and very effective. Here’s how you can use it:

1. First, place the midpoint of the protractor at the vertex of the angle.
2. Make sure one side of the angle lines up with the zero line on the protractor.
3. Look at where the other side of the angle meets the protractor. The number it points to is the angle’s measurement.

Using a protractor is quick and gives you a precise measurement. I remember using a protractor in school; it was always my go-to tool for geometry homework.

Ruler And Compass

The ruler and compass method is a bit more hands-on but equally useful. Here’s a step-by-step guide:

• Draw a baseline: Use the ruler to draw a straight line. This will be one side of your angle.
• Set the compass: Place the compass point on one end of the baseline and draw an arc that intersects the baseline.
• Mark the arc: Without changing the compass width, place the compass point where the arc intersects the baseline and draw another arc.
• Draw the second line: Use the ruler to draw a line from the vertex through the new intersection point. The angle between the baseline and this new line is your measured angle.

This method might seem tricky at first, but with practice, it becomes easier. I recently showed this technique to my younger cousin, and he found it quite fun to draw the arcs and see the angles come to life.

So there you have it—two basic tools for measuring angles in a polygon. Whether you choose a protractor or a ruler and compass, both methods will help you get accurate results. Happy measuring!

Sum Of Interior Angles

Understanding how to measure angles in a polygon is essential. Every polygon has interior angles, which are the angles inside the shape. The sum of these interior angles varies depending on the number of sides the polygon has. Knowing this sum helps in solving geometry problems and understanding shapes better.

Formula For Calculation

The formula for calculating the sum of interior angles is simple. For any polygon, you can use this formula: (n – 2) × 180°. Here, n represents the number of sides in the polygon. By subtracting 2 from the number of sides and then multiplying by 180 degrees, you get the sum of all interior angles.

Examples And Practice Problems

Let’s look at some examples. A triangle has three sides. Using the formula: (3 – 2) × 180° = 180°. So, the sum of interior angles in a triangle is 180 degrees.

For a square, which has four sides: (4 – 2) × 180° = 360°. So, the sum of interior angles in a square is 360 degrees.

Now, try this practice problem. Find the sum of interior angles of a pentagon. A pentagon has five sides. Using the formula: (5 – 2) × 180° = 540°. So, the sum of interior angles in a pentagon is 540 degrees.

Practice another one. Calculate the sum of interior angles of a hexagon. A hexagon has six sides. Using the formula: (6 – 2) × 180° = 720°. So, the sum of interior angles in a hexagon is 720 degrees.

These examples show how easy it is to use the formula. Practice with different polygons. This will help you get better at measuring angles in polygons.

Exterior Angle Theorem

The Exterior Angle Theorem is a fundamental concept in geometry. It states that the exterior angle of a polygon is equal to the sum of its remote interior angles. This theorem helps in understanding the properties of polygons. It is vital for calculating angles and solving geometric problems.

Explanation Of Theorem

The Exterior Angle Theorem states that the exterior angle of a polygon equals the sum of the two opposite interior angles. This works for any polygon, whether it’s a triangle, quadrilateral, or any other multi-sided shape. For example, in a triangle, the exterior angle is equal to the sum of the two non-adjacent interior angles. This relationship simplifies the process of finding unknown angles in polygons.

This theorem has many practical uses. Architects use it to design buildings. Engineers rely on it for constructing bridges. It also helps in navigation and mapping. By knowing exterior angles, one can easily determine interior angles. This knowledge is crucial in fields that require precise measurements and calculations.

Credit: www.youtube.com

Measuring Angles In Regular Polygons

Hey friends! Today, we’re diving into the exciting world of measuring angles in regular polygons. It’s easier than you think, and by the end of this, you’ll be able to measure these angles with ease. Whether you’re working on a school project, designing something cool, or just curious, this guide will help you understand it all. Ready? Let’s go!

Equal Angle Calculation

First things first, let’s talk about equal angles. In regular polygons, all angles are equal. This makes things super simple. Imagine a pizza cut into equal slices. If you know how many slices there are, you can figure out the angle of each slice. The same goes for polygons!

Here’s a quick formula to calculate the measure of each angle in a regular polygon:

• Count the number of sides (n).
• Use the formula: (n-2) × 180° / n

Let’s break it down with an example. Suppose you have a regular pentagon (5 sides):

Number of Sides (n)	5
Formula	(5-2) × 180° / 5
Calculation	3 × 180° / 5 = 540° / 5 = 108°
Each Angle	108°

See how simple that was? You just need to plug in the number of sides, do a bit of multiplication and division, and voila! You have the measure of each angle.

Step-by-step Guide

Now, let’s go through a step-by-step guide to measuring angles in regular polygons. Follow these easy steps:

1. Identify the Polygon: Determine the number of sides your polygon has. Is it a triangle, square, hexagon, etc.?
2. Use the Formula: Remember the formula we talked about earlier: (n-2) × 180° / n. Plug in the number of sides.
3. Calculate: Do the math. Multiply (n-2) by 180° and then divide by the number of sides (n).
4. Check Your Work: Ensure your calculation is correct. If your polygon has 6 sides, each angle should be 120° (as shown in our example).

Let’s try another example together. Suppose you have a regular hexagon (6 sides):

• Number of sides (n) = 6
• Formula: (6-2) × 180° / 6
• Calculation: 4 × 180° / 6 = 720° / 6 = 120°
• Each angle = 120°

Easy, right? With these steps, you can measure angles in any regular polygon. It’s like riding a bike – once you get the hang of it, it becomes second nature.

I remember when I first learned this formula. It felt like unlocking a secret code. I used to double-check my work a million times because it seemed too simple. But trust me, it works every time!

So, next time you need to measure angles in a regular polygon, you know what to do. Happy measuring!

Measuring Angles In Irregular Polygons

Hey there! Ever wondered how to measure angles in polygons that are not perfect shapes? Like those odd, irregular polygons? It can feel tricky, right? But don’t worry. Today, we will break it down into simple steps. You’ll see it’s easier than you think.

Dividing Into Triangles

The first method is to divide the polygon into triangles. Why triangles? Because they are the simplest shapes for measuring angles. Here’s how you can do it:

• Pick one vertex (corner) of the polygon.
• Draw lines from this vertex to all other non-adjacent vertices.
• Now, your polygon is divided into several triangles.

Once you have your triangles, measuring angles becomes straightforward. You can use a protractor or simple geometry rules. Remember, the sum of angles in a triangle is always 180 degrees. So, if you know two angles, you can easily find the third one.

Using Trigonometry

Another method is using trigonometry. Sounds complicated? It’s not. Trigonometry is just a fancy word for measuring angles using sides of a triangle. Let’s simplify it:

1. First, divide your polygon into triangles like we did before.
2. For each triangle, measure the lengths of all sides.
3. Use the trigonometric ratios (sine, cosine, or tangent) to find the angles.

Here’s a quick tip: Sine is useful when you know the opposite side and hypotenuse. Cosine helps when you know the adjacent side and hypotenuse. Tangent is great for the opposite and adjacent sides.

For example, if you know the sides of a triangle, you can use the cosine rule to find an angle:

cos(θ) = (a² + b² - c²) / (2ab)

Where a, b, and c are the lengths of the sides, and θ is the angle opposite side c.

So, that’s it! Measuring angles in irregular polygons doesn’t have to be daunting. Whether you divide the shape into triangles or use trigonometry, these methods make it manageable. Go ahead, give it a try!

Expert Tips For Accurate Measurement

Learn how to measure angles in a polygon accurately. Use a protractor to find each angle’s degree. Always double-check your measurements for precision.

Measuring angles in a polygon can seem tricky. But with the right tips, it becomes easy. Accurate measurements ensure your projects are precise. Let’s explore some expert tips to help you measure angles accurately.

Common Mistakes To Avoid

Avoid using worn-out protractors. They can give incorrect readings. Ensure your tools are in good condition. Do not guess the measurements. Always use a reliable method. Rushing through the process often leads to errors. Take your time for each measurement.

Advanced Tools And Techniques

Digital protractors offer more precision. They display angles in digital format. Laser angle finders are also helpful. They use laser beams to measure angles. For complex polygons, use software tools. They can calculate angles with high accuracy. Practice using these tools to improve your skills. “`

Practical Applications

Hey friends, ever wondered how measuring angles in polygons can be super useful in real life? Measuring angles isn’t just for math class. It has many practical applications that can make a big difference in various fields. Let’s dive into some of these practical uses and see how knowing your angles can come in handy.

Architectural Design

In architectural design, precision is key. Architects need to measure angles to create accurate blueprints and designs for buildings. Imagine you are designing a new house. You want to make sure every corner is just right. Measuring angles helps you:

• Ensure walls meet at the correct points
• Create aesthetically pleasing spaces
• Maximize the use of space efficiently

I remember helping a friend design their dream home. We measured every angle to make sure the living room had perfect symmetry. It made a huge difference in how the space felt.

Engineering Projects

Engineering projects also rely heavily on accurate angle measurements. Whether it’s constructing a bridge or designing a new gadget, engineers need to know their angles. Here’s why:

• Safety: Proper angles ensure structures are stable and safe.
• Functionality: Correct angles make sure parts fit together perfectly.
• Efficiency: Reducing waste by cutting materials at the right angles.

Think about building a bridge. If the angles are off, the bridge might not hold up under pressure. That could be dangerous. Engineers use angles to make sure everything is strong and secure.

So, next time you think about angles, remember they are not just for math tests. They play a huge role in making our world safe and beautiful. From homes to bridges, knowing how to measure angles in polygons can make a real difference.

Conclusion And Further Reading

Explore practical techniques for measuring angles in polygons. Check out recommended resources for deeper learning on this topic.

Understanding how to measure angles in a polygon is essential for geometry. This knowledge is useful in various real-life applications. From architecture to art, accurate angle measurement is crucial.

Summary Of Key Points

To measure angles in a polygon, start by knowing the polygon type. Remember, the sum of interior angles depends on the number of sides. For example, a triangle’s angles sum up to 180 degrees. A quadrilateral’s angles add up to 360 degrees. Use a protractor for precise angle measurement. Practice with different polygons to enhance your skills.

Recommended Resources

For deeper understanding, check out these resources: – “Geometry for Beginners” by Lisa Anderson – Khan Academy’s free geometry courses – MathIsFun.com for interactive lessons – “Practical Geometry” videos on YouTube These resources provide detailed explanations and exercises. They will help you gain confidence in measuring angles. Keep practicing to improve your proficiency. “`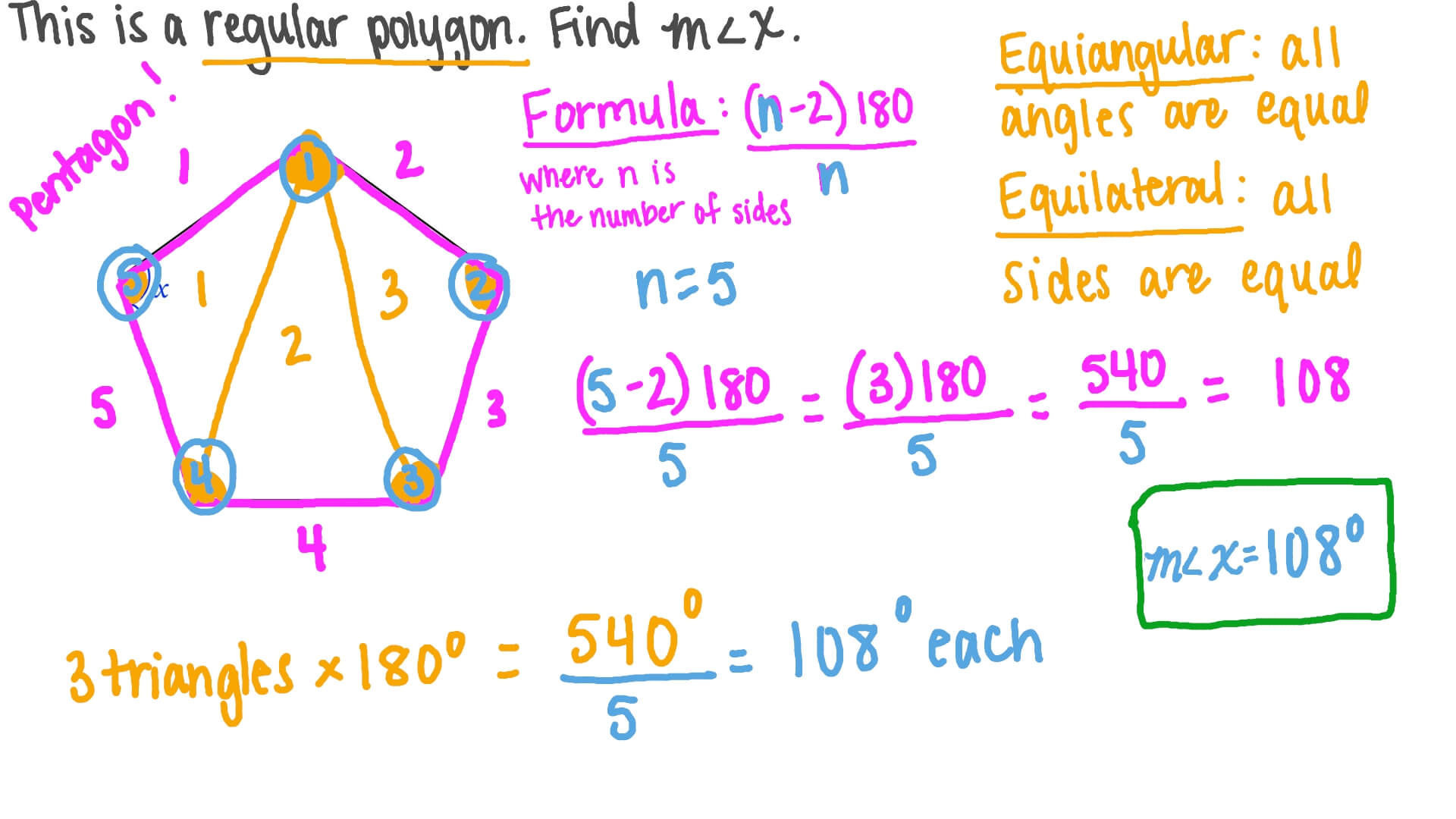

Credit: www.nagwa.com

Frequently Asked Questions

Do All Angles In A Polygon Add Up To 360°?

No, only the exterior angles of a polygon add up to 360°. Interior angles sum varies based on the number of sides.

Do Angles In A Polygon Add Up To 180°?

No, angles in a polygon do not add up to 180°. Only a triangle’s angles sum to 180°. For polygons, the sum is (n-2)×180°, where n is the number of sides.

How Do You Find The Number Of Angles In A Regular Polygon?

To find the number of angles in a regular polygon, count its sides. A polygon with n sides has n angles.

How Do You Find The Angles Of An Irregular Polygon?

To find angles of an irregular polygon, divide it into triangles. Sum the interior angles of each triangle, then sum these totals. Subtract the sum from 360 degrees if dealing with exterior angles. This helps determine individual angles accurately.

Conclusion

Understanding how to measure angles in a polygon is essential. It helps in various fields like geometry, engineering, and art. Start by knowing the types of polygons. Then, use simple formulas to find interior and exterior angles. Practice makes perfect.

Use tools like protractors for accuracy. Remember, learning this skill improves problem-solving abilities. Keep practicing, and soon it will feel natural. With time, you’ll measure angles with ease. Happy learning!