When dealing with vectors, understanding how to determine both the speed and direction is crucial. Whether you are studying physics, mathematics, or engineering, knowing how to find these components can help you analyze motion and forces accurately.
Credit: www.youtube.com
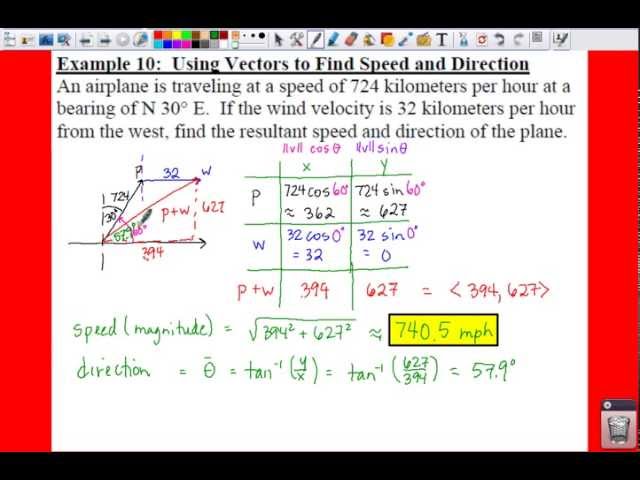
Finding Speed and Direction of a Vector
There are specific steps you can follow to calculate the speed and direction of a vector:
- Determine the x and y components of the vector.
- Calculate the magnitude of the vector using the x and y components.
- Find the angle the vector makes with the x-axis.
- Use trigonometric functions to find the direction of the vector.
Credit: study.com
Calculating Speed and Direction
Speed and direction are essential when working with vectors. By following these steps, you can easily find both components accurately:
| Step | Description |
|---|---|
| 1 | Determine the x and y components of the vector. |
| 2 | Calculate the magnitude of the vector using the x and y components. |
| 3 | Find the angle the vector makes with the x-axis. |
| 4 | Use trigonometric functions to find the direction of the vector. |
Example Calculation
Let’s consider a vector with x-component 3 and y-component 4. To find its speed and direction:
- Calculate the magnitude: \( |\vec{v}| = \sqrt{3^2 + 4^2} = 5 \).
- Find the angle: \( \theta = \arctan(\frac{4}{3}) \approx 53.13^\circ \).
- Therefore, the speed is 5 units, and the direction is approximately 53.13 degrees from the positive x-axis.
Applications in Real Life
Understanding how to find the speed and direction of a vector is essential in various fields:
- In physics, it helps in analyzing the motion of objects.
- In engineering, it is crucial for designing structures and analyzing forces.
- In mathematics, it is used in calculus and geometry for various calculations.
Frequently Asked Questions
How Do You Find The Direction Of A Vector?
To find the direction of a vector, use the formula: angle = arctan(y/x). This gives the angle rotating anti-clockwise from the x-axis.
What Is The Formula For The Speed Of A Vector?
The formula for the speed of a vector is the magnitude of the velocity, given by Speed = ||v(t)|| = ||r'(t)||.
How To Determine Speed And Direction?
To determine speed and direction, calculate the magnitude and angle of the vector using trigonometry formulas.
How To Find Resultant Speed And Direction Vectors?
To find resultant speed and direction vectors, use vector addition to combine individual velocities. Calculate the magnitude and angle of the resultant vector using trigonometric functions. This method applies to both linear and angular velocities, aiding in solving various physics and engineering problems.
Conclusion
Mastering the skill of finding the speed and direction of a vector is fundamental for anyone dealing with vectors. By following the steps outlined above and practicing with examples, you can enhance your understanding of vectors and their applications in different disciplines.
Rakib Sarwar is a seasoned professional blogger, writer, and digital marketer with over 12 years of experience in freelance writing and niche website development on Upwork. In addition to his expertise in content creation and online marketing, Rakib is a registered pharmacist. Currently, he works in the IT Division of Sonali Bank PLC, where he combines his diverse skill set to excel in his career.