Angles and arcs are crucial parts of a circle. They have a unique and important relationship.
Understanding the connection between angles and arcs can make geometry easier. In a circle, the angle formed by two radii creates an arc. The size of this angle directly affects the arc’s length. This relationship is key to solving many geometric problems.
With a clear grasp of this concept, you can tackle questions about circles with confidence. Dive in to learn more about how angles and arcs interact within a circle. This knowledge will help you in both math classes and real-life applications.
Introduction To Angles And Arcs
Understanding the relationship between angles and arcs in a circle is essential in geometry. Angles and arcs are fundamental concepts that help us describe and analyze circular shapes. Let’s dive into their definitions and importance.
Basic Definitions
An angle is formed by two rays that share a common endpoint called the vertex. In a circle, angles can be measured in degrees or radians. Arcs are portions of the circumference of a circle. They can be small or large, depending on the angle they subtend at the center of the circle.
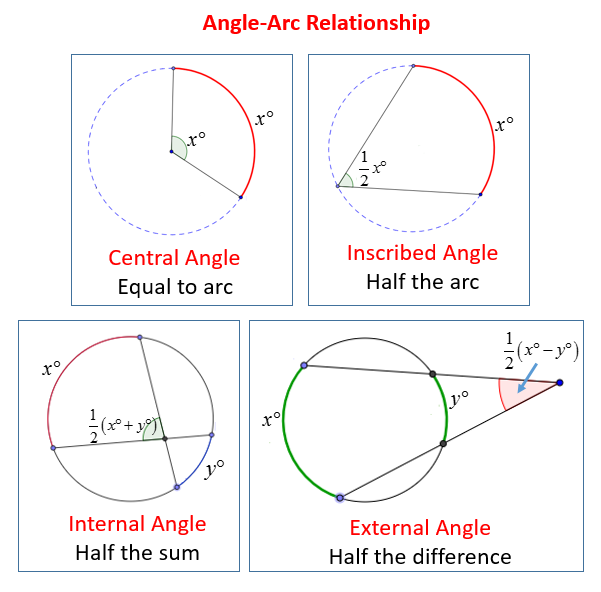
An angle in a circle can be central or inscribed. A central angle has its vertex at the center of the circle. An inscribed angle has its vertex on the circle itself. The size of the arc depends on the angle, making their relationship crucial.
Importance In Geometry
Angles and arcs are key to solving many geometric problems. They help us understand properties of circles and their segments. For instance, the length of an arc is proportional to the angle it subtends. This principle simplifies calculations and helps in real-world applications.
Understanding angles and arcs also aids in solving problems involving sectors and segments. Sectors are parts of a circle, bounded by two radii and an arc. Segments are areas bounded by a chord and an arc. Mastering these concepts provides a solid foundation for further geometric studies.

Credit: www.nagwa.com
Central Angles
Central angles play a key role in understanding circles. They help explain the connection between angles and arcs. A central angle has its vertex at the center of the circle. Its sides extend to touch the circle, creating an arc.
Definition And Properties
A central angle is formed by two radii of a circle. The measure of the central angle equals the measure of the arc it creates. This makes understanding arcs easier.
Central angles have unique properties. One important property is that the sum of all central angles in a circle is 360 degrees. Each central angle represents a portion of the circle. This makes calculations straightforward.
Examples In Real Life
Central angles are seen in everyday life. For instance, pizza slices represent central angles. Each slice forms an angle at the center, creating an arc on the edge.
Clocks also show central angles. The hands of a clock create central angles as they move. This helps in reading time accurately. Another example is in pie charts. Each section of the chart forms a central angle, representing data clearly.
Inscribed Angles
Inscribed angles in a circle create fascinating relationships between angles and arcs. They are essential in understanding the geometry of circles. These angles provide insight into how a circle’s parts relate to one another.
Definition And Properties
An inscribed angle has its vertex on the circle. Its sides are chords of the circle. The measure of an inscribed angle equals half the measure of its intercepted arc. If the arc measures 80 degrees, the inscribed angle will measure 40 degrees. Inscribed angles subtending the same arc are equal. This property helps in solving various geometric problems.
Comparing With Central Angles
Central angles have their vertex at the center of the circle. The sides extend to the circle’s circumference. The measure of a central angle equals the measure of its intercepted arc. If the arc measures 80 degrees, the central angle will also measure 80 degrees. This is a key difference from inscribed angles.
While inscribed angles are half the arc measure, central angles match the arc measure. Understanding these differences is crucial. It helps in solving complex geometric problems involving circles.
Measuring Arcs
Hey friends, today we’re diving into a fascinating topic: the relationship between angles and arcs in a circle. Specifically, we’ll focus on measuring arcs. Understanding how to measure arcs is essential for anyone studying circles. Let’s break it down step by step.
Arc Length
Measuring the arc length is like measuring the distance along the curved line of the circle. It’s different from measuring straight lines. Here’s a simple way to think about it. Imagine the arc as a piece of a pie. The bigger the piece, the longer the arc length.
There are a few things we need to measure an arc length:
- The radius of the circle
- The central angle (the angle that the arc subtends at the center of the circle)
The formula for calculating arc length is:
Arc Length = (Central Angle / 360) 2π RadiusLet’s say we have a circle with a radius of 5 units and a central angle of 60 degrees. Plugging these into our formula, we get:
Arc Length = (60 / 360) 2π 5 = (1/6) 10π ≈ 5.24 unitsSimple, right? This formula helps us understand how the arc length changes with different angles and radii.
Relation To Radius
The radius plays a key role in determining the arc length. Think of the radius as the length of a spoke in a wheel. The longer the spoke, the bigger the wheel, and thus, the longer the arc for any given angle.
Here are some points to remember about the relationship between the radius and the arc length:
- A larger radius means a longer arc for the same angle.
- A smaller radius means a shorter arc for the same angle.
- The arc length is directly proportional to the radius.
Let’s consider an example. Imagine two circles, one with a radius of 3 units and another with a radius of 6 units. If both have a central angle of 45 degrees, the arc lengths will be:
- For the circle with a radius of 3 units: (45 / 360) 2π 3 ≈ 2.36 units
- For the circle with a radius of 6 units: (45 / 360) 2π 6 ≈ 4.71 units
As you can see, doubling the radius from 3 to 6 units also doubles the arc length from 2.36 units to 4.71 units.
I hope this makes the concept of measuring arcs clearer. It’s amazing how interconnected these elements of a circle are!
Arc And Angle Relationships
Understanding the relationship between angles and arcs in a circle can help in solving many geometric problems. This relationship forms the basis of many theorems and mathematical applications. Let’s explore how angles and arcs interact within the confines of a circle.
Angle-arc Theorem
The Angle-Arc Theorem states that the measure of a central angle is equal to the measure of the arc it intercepts. This means if you have a central angle of 60 degrees, the arc it intercepts will also measure 60 degrees. It’s a straightforward yet powerful concept in circle geometry.
For instance, consider a circle with a central angle of 90 degrees. The arc opposite to this angle will also be 90 degrees. This theorem simplifies many calculations and helps in understanding other geometric principles.
Applications In Problems
The Angle-Arc Theorem is often used in various geometric problems. For example, it helps in finding unknown angles or arc lengths. If you know one measure, you can easily find the other.
In real-world applications, this relationship aids in design and engineering. For instance, in architecture, understanding these principles ensures accurate construction of circular structures. It also helps in fields like astronomy, where the angles and arcs of celestial circles are crucial.
By mastering the basic concepts of angles and arcs in a circle, solving complex problems becomes easier. This knowledge is not just academic but has practical uses in everyday life.
Credit: www.onlinemathlearning.com
Sector Of A Circle
Hey there! Today, let’s dive into the fascinating world of circles, focusing on a part called the sector of a circle. If you’ve ever wondered how angles and arcs relate in a circle, you’re in the right place. A sector is like a slice of pizza. It’s that piece of the circle that you get when you cut it from the center to the edge. Let’s explore this concept more deeply.
Definition And Formula
A sector of a circle is the area enclosed by two radii and the arc between them. Think about it as a ‘pie slice’ of the circle. The size of the sector depends on the angle at the center (called the central angle) and the radius of the circle.
Here’s a simple formula to find the area of a sector:
Area of a Sector = (θ/360) π r²
Where:
- θ is the central angle in degrees
- π (Pi) is approximately 3.14159
- r is the radius of the circle
For example, if you have a circle with a radius of 4 cm and a central angle of 90 degrees, the area of the sector would be:
Area = (90/360) π 4² = (1/4) π 16 = 4π cm²
Difference From Segment
It’s easy to confuse a sector with a segment, but they’re different. A segment is the area between a chord and the arc. Imagine a chord as a straight line cutting through the circle, not passing through the center. The segment is the area between this chord and the arc above it.
Here’s a quick comparison:
| Sector | Segment |
|---|---|
| Formed by two radii and an arc | Formed by a chord and an arc |
| Includes the center of the circle | Does not include the center |
| Looks like a ‘pie slice’ | Looks like a ‘curved triangle’ |
Understanding the difference helps in solving geometry problems more accurately. Next time you see a sector or segment, you’ll know exactly what it is!
So, there you have it! The sector of a circle is a simple yet crucial concept in geometry. It’s all about understanding the parts of the circle and how they work together. Keep practicing, and soon, circles will be as easy as pie. Happy learning!
Real-world Applications
Understanding the relationship between angles and arcs in a circle helps in navigation and engineering. This concept aids in calculating distances and constructing various structures. Clear comprehension of this relationship is vital for accurate designs and measurements.
Hey friends, today we’re diving into something really cool: the relationship between angles and arcs in a circle. You might think it’s all about math class, right? Nope! These concepts are everywhere in our lives. Let’s see how they fit into some real-world applications.Engineering
In engineering, understanding angles and arcs is super important. Imagine building a bridge. Engineers need to know the exact angles to make sure the structure is stable. They also use arcs to design roads and tunnels. Example: When designing a curved road, engineers calculate the arc length to determine how much material they need. They measure angles to make sure the curve is safe for cars to turn. Here’s a quick table to show you how angles and arcs are used in different engineering projects:| Project | Use of Angles | Use of Arcs |
|---|---|---|
| Bridge | Calculating support angles | Designing curved sections |
| Road | Measuring turn angles | Determining arc lengths |
| Tunnel | Aligning entrance angles | Creating circular paths |
Astronomy
In astronomy, angles and arcs help us understand the night sky. Astronomers use them to track the movement of planets and stars. Example: When you look at the moon, it seems to move across the sky, right? Astronomers calculate the angle of this movement to predict its path. They also measure the arc of its orbit around the Earth. Here are a few ways angles and arcs are used in astronomy:- Measuring the angle between stars to navigate space.
- Calculating the arc of a planet’s orbit to predict its position.
- Tracking the moon’s phases using angles and arcs.

Credit: www.youtube.com
Common Misconceptions
Angles and arcs in a circle have a unique relationship. An angle’s size directly impacts the length of its corresponding arc. Understanding this helps in solving geometric problems easily.
Hey friends, today we’re diving into a topic that often confuses many of us: the relationship between angles and arcs in a circle. It’s easy to get mixed up, but don’t worry! We’ll break it down into simple terms and clear up some common misconceptions.Misunderstanding Measurements
One big misconception is how we measure angles and arcs. You might think they’re the same thing. But, they’re not. An angle is measured in degrees or radians. For example, a right angle is 90 degrees. On the other hand, an arc is a part of the circle’s circumference. It is measured by its length. Let’s say you have a pizza. If you cut a slice, the angle is the pointy part of the slice. The arc is the curved crust. Here’s a quick table to help:| Measurement | Unit |
|---|---|
| Angle | Degrees or Radians |
| Arc | Length (usually in cm or inches) |
Incorrect Assumptions
Another mistake is thinking that a bigger angle always means a longer arc. Not true! The length of the arc depends on the radius of the circle too. Let’s break it down: 1. Small Circle, Big Angle: You could have a big angle, but if the circle is small, the arc is short. 2. Big Circle, Small Angle: Or you might have a small angle, but if the circle is big, the arc is long. So, always remember: both the angle and the radius matter. Example: Imagine two ferris wheels. One is small, the other is huge. If both have cars at a 45-degree angle from the center, the path (arc) the cars travel will be different. The one on the larger ferris wheel travels a longer arc. Anecdote: I once tried explaining this to my nephew using a protractor and a string. He got it right away when he saw the string’s length changing with different sized circles. He said, “Oh! It’s like walking a bigger circle makes you walk more!” So, next time you think about angles and arcs, remember these points. They’ll make it a lot easier to understand! “`Frequently Asked Questions
What Is The Relationship Between Arc And Angle?
An arc is a portion of the circumference of a circle. An angle measures the space between two intersecting lines or surfaces at the point where they meet. The length of an arc is directly proportional to the measure of the central angle.
What Is The Relationship Between Angles And Circles?
Angles and circles are closely related. Angles can be measured using the arc of a circle. Central angles have their vertex at the circle’s center. Inscribed angles have their vertex on the circle.
What Is The Rule For Angles And Arcs Of A Circle?
Angles at the center of a circle are twice the angles at the circumference. Arcs are proportional to their corresponding angles.
What Is The Relationship Between Circle And Arc?
A circle is a closed curve with all points equidistant from the center. An arc is a segment of the circle’s circumference.
Conclusion
Understanding the relationship between angles and arcs in a circle is key. It helps in geometry and many practical applications. By knowing these basics, you can solve various problems. Remember, angles and arcs are interconnected. Their properties are useful in calculations and design.
Keep practicing these concepts for better grasp. This knowledge can improve your math skills. Stay curious and keep learning. Circles are more interesting than they seem. Enjoy exploring their secrets!
